[자료구조] 힙(Heap)

Heap

최대값, 혹은 최소값을 빠르게 찾기 위한 자료구조이며,

일반적으로 완전이진트리를 활용하여 구현하고, 우선순위 큐에 사용한다.

 

우선순위 큐란

FIFO구조의 일반적인 큐가 아니라, 각 데이터에 우선순위가 있어서, 

우선순위가 높은 데이터가 먼저 POP되는 자료형태이다.

 

예를 들어 운영체제에서 프로그램들을 스케쥴링 할 때,

FIFO방식으로 프로세스를 처리한다면, 처리시간이 긴 프로세스를 처리하는 동안 처리시간이 짧은 프로세스는 대기시간이 길어지게 되고, 이는 비효율적이다.

따라서 처리시간이 짧은 프로세스에 높은 우선순위를 두어 이를 먼저 처리하고, 처리시간이 긴 프로세스를 나중에 처리하려고 할 때 우선순위 큐를 사용할 수 있다.

 

Heap의 구조

힙은 두가지로 나뉜다. 루트노드가 가장 작은 값인 Min Heap과 그 반대의 Max Heap이다.

이진트리와 마찬가지로 서브트리들도 힙의 조건을 만족한다.

 

서브트리의 모든 값은 루트노드보다 작기만 하면 되기 때문에 정렬 상태는 아니지만,

루트노드를 하나씩 추출해서 저장한다면 Heap전체의 최소값들을 순서대로 저장하게 되므로 정렬이 된다.

이를 힙 정렬(Heap Sort)이라 한다.

 

Heap의 구현

이러한 힙은 자식노드의 값을 왼쪽부터 채우는 완전 이진 트리의 형태이기 때문에 선형 자료구조로 표현할 수 있다.

위와 같은 맥스 힙이 있다고 할 때, 이를 선형 자료구조로 생각해보면,

편의상 인덱스 0번을 비워두고 1번부터 값을 채웠다고 할 때, 

부모 노드의 인덱스를 $i$라 하면 자식노드의 인덱스는 $2i$와 $2i+1$이 된다.

이를 활용하면 노드에 따른 자식노드와 부모노드의 관계가 명확해지므로 힙을 쉽게 구현할 수 있다.

 

값 삭제

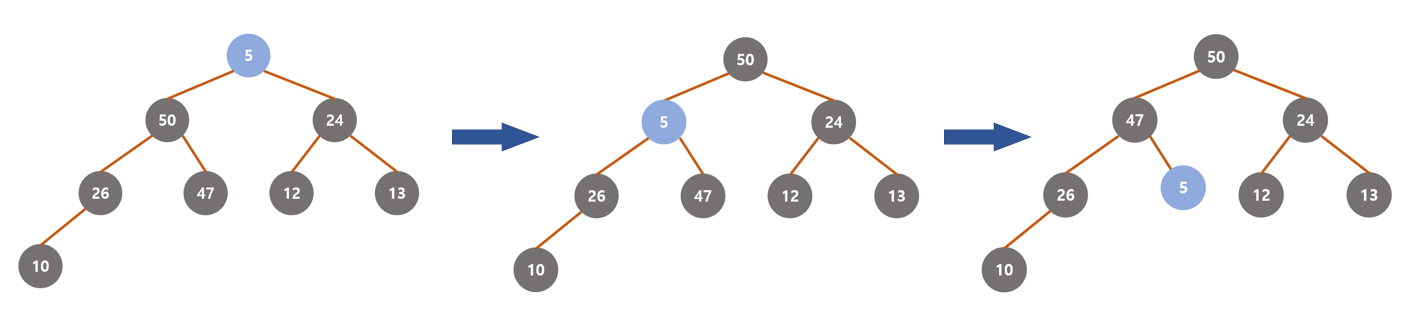
힙은 우선순위가 높은 값을 추출하는데에 의의가 있으므로, 루트노드의 값을 추출한다.

그 후에 힙의 형태를 유지하기 위해서 전체 힙의 마지막 노드(위 그림 기준 인덱스가 9이고 값이 5인)를

루트노드로 옮기고, 자식노드와 비교하면서 자식 노드 중 큰 값과 위치를 바꾸며 내려간다.

 

값 추가

값을 추가할 때는 리스트의 마지막에 값을 추가하고, 부모노드와 비교하면서 값을 바꿔준다.

 

이러한 연산에서 힙의 장점이 드러나는데, 

정렬된 리스트에서 값을 삽입할때는 O(n), 삭제할때는 O(1)이 걸리고,

정렬되지 않은 리스트에서 값을 삽입 학제할 때는 각각 O(1), O(n)이 걸린다.

힙의 경우에는 둘 모두 O(log n)으로 삽입 삭제 모두를 사용할 경우 좀 더 효율적이다.

코드

직접 힙을 구현한 코드는 다음과 같다.

class Heap:
    def __init__(self):
        self.heap_list = [None]

    def insert(self, data):
        if len(self.heap_list) == 1:
            print(1)
            self.heap_list.append(data)

        else:
            self.heap_list.append(data)
            idx = len(self.heap_list) - 1

            while 1:
                p_idx = idx // 2
                if p_idx != 0 and self.heap_list[idx] > self.heap_list[p_idx]:
                    self.heap_list[idx], self.heap_list[p_idx] = self.heap_list[p_idx], self.heap_list[idx]
                    idx = p_idx
                else:
                    break

    def delete(self):
        data = self.heap_list[1]
        idx = len(self.heap_list) - 1
        self.heap_list[1] = self.heap_list[idx]
        self.heap_list.pop(-1)
        idx = 1

        while 1:
            print(self.heap_list)
            left_idx = 2*idx
            right_idx = 2*idx + 1

            if left_idx >= len(self.heap_list):
                break
            elif right_idx >= len(self.heap_list):
                if self.heap_list[idx] < self.heap_list[left_idx]:
                    self.heap_list[idx], self.heap_list[left_idx] = self.heap_list[left_idx], self.heap_list[idx]
                break
            else:
                if self.heap_list[left_idx] > self.heap_list[right_idx]:
                    if self.heap_list[left_idx] < self.heap_list[idx]:
                        break
                    self.heap_list[idx], self.heap_list[left_idx] = self.heap_list[left_idx], self.heap_list[idx]
                    idx = left_idx
                else:
                    if self.heap_list[right_idx] < self.heap_list[idx]:
                        break
                    self.heap_list[idx], self.heap_list[right_idx] = self.heap_list[right_idx], self.heap_list[idx]
                    idx = right_idx

 

물론 우리의 파이썬은 모듈을 제공한다.

바로 heapq라는 모델인데, 최소힙을 기반으로 구현되어있다.

따라서 최대힙으로 바꾸려면 -1을 곱해서 연산을 진행하면 최대힙처럼 사용할 수 있다.

import heapq

heap = []
heapq.heappush(heap, 5)
heapq.heappush(heap, 7)
heapq.heappush(heap, 3)
heapq.heappush(heap, 9)
print(heap)

heapq.heappop(heap)
heapq.heappop(heap)
print(heap)

https://docs.python.org/ko/3/library/heapq.html

heapq — 힙 큐 알고리즘 — Python 3.10.2 문서

여기를 참고하면 다양한 메서드를 확인할 수 있다.